“Más vale dólar en mano que cien volando”
La economía es dinámica de por sí por su expansión o contracción, pero a esto hay que sumarle que el valor del dinero fluctúa en el tiempo, tendiendo a devaluarse, es decir que cada vez podemos comprar menos con $100, por ejemplo.
Para “combatir” esto los actores del mercado financiero se ponen en campaña para “hacer trabajar” el dinero, colocando el dinero en diferentes actividades/activos para obtener un retorno, peleando contra esa devaluación, contra la inflación y en el caso de inversionistas profesionales, tratando de batir el mercado.
Detrás del objetivo de “maximizar retornos” existe la amenaza de que al estar “quieto” bajo el colchón el dinero no solo no generará retorno, sino que perderá valor.
Estos son conceptos fundamentales para entender la variación del dinero en el tiempo.
Valor Presente
Es el valor del dinero hoy, en este momento. Este concepto nos permite “descontar” toda esa influencia que el tiempo tendrá sobre el dinero a través de las tasas que intervienen (interés, rentabilidad, inflación, etc.) y saber cuánto vale el día de hoy.
También nos permite determinar cuánto debo invertir hoy para lograr un monto específico mañana.
Por ejemplo:
Para que mis hijos vayan a la universidad debo contar con $40,000 y poder pagar toda la colegiatura. Esta inversión estará inmóvil durante los próximos 15 años (15 períodos) y espero que el dinero tenga una tasa de retorno de 8%. ¿Cuánto dinero debo invertir hoy para lograr ese objetivo?
La fórmula del Valor Presente es:
VP = VF / (1+ r)^i
Donde:
VP es el valor presente
VF es el valor futuro, en este caso $40,000
r es el número de períodos
i la tasa de interés o de retorno en este caso
Haciendo el cálculo, para lograr mi objetivo yo debo invertir hoy $12,610.
Se hicieron muchos supuestos, como que el precio de la colegiatura será el mismo en 15 años, pero este ejemplo sirve para ilustrar nuestro punto.
Valor Futuro
Por otro lado, si cuento con dinero hoy, y se presenta ante mí una oportunidad de inversión puedo aplicar la misma lógica para conocer cuánto valdrá esa inversión en un tiempo definido.
Ejemplo: Tengo $10,000 en mi cuenta, y se presenta un amigo con una posible inversión en bonos con una tasa de retorno de 7% por 12 años. ¿Cuánto valdrá mi dinero luego de ese tiempo?
La fórmula es:
VF = VP * (1+r)^i
Donde las variables son las mismas que para el cálculo del valor presente.
En nuestro ejemplo, la oportunidad de inversión representa: $25,182 luego de los 12 años en los que recibiré de vuelta mi dinero además de las ganancias.
Conocer esto me permite sopesar posibilidades, puedo comparar opciones para determinar cuál es la que más me conviene. Claro que hay que añadir otras variables como el riesgo, por ejemplo, pero me permite tomar una mejor decisión sabiendo el valor final que esperaré recibir luego de ese tiempo.
Interés Compuesto
El famoso interés compuesto, poderoso por sus cualidades de replicarse sobre su valor original y todo lo que va generando. ¿Qué significa esto?
Es sencillo:
Tengo $100 y los invierto a un año a una tasa de 10% à Tendré al final del año $110, mis $100 originales y $10 que se generaron gracias a la tasa a la que invertí el dinero.
Ahora tengo $110 y los invierto otro año a una tasa de los mismos 10% à Tengo ahora $121, mis $110 originales más $11 de la tasa de retorno. Noto que ahora el interés ya no genera $10 sino $11.
Para terminar mi ejemplo, tengo $121 e invierto nuevamente otro año a $10 à Tengo ahora $133.1, mis $121 originales más $12.1 de intereses.
¿Qué puedo notar de esto? Que, al sumar las ganancias a la inversión, la misma tasa (10% en este caso) cada vez genera más. Ese es el poder del interés compuesto.
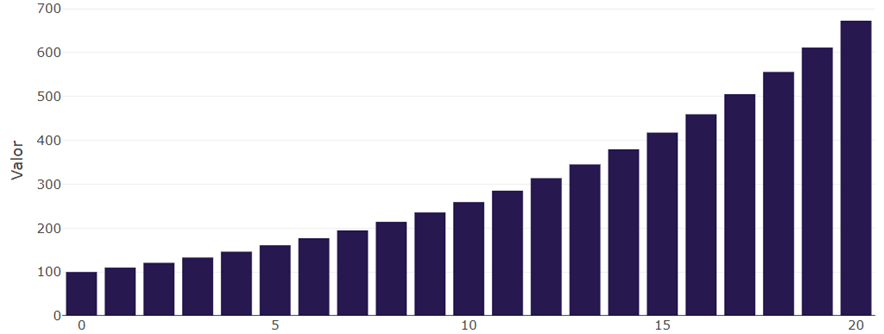
Lo que pocos mencionan es que para que funcione hay que evitar hacer retiros. Dejar que la bola de nieve ruede sin quitarle ni un poco de lo que la compone permite que cada vez acumule más nieve (ganancias).
Noto que siguiendo el ejemplo de $100 a 10% pero a 20 años, el valor de mi inversión alcanza alrededor de $650. ¡Un incremento de más de 5 veces!
A simple vista puedo decir: “Un rendimiento de 550%, increíble” Pero esta apreciación es errónea, el interés compuesto fue del 10% anual. Y ese es el poder del interés compuesto.
¿Las inversiones más eficientes según un estudio? Tener mi propia empresa, la ganancia de capital y los dividendos, junto con la escalabilidad potencian el interés compuesto.
Ilustro este último punto con un ejemplo que vi de primera mano:
Tengo $30,000 de capital propio y abro mi negocio. Me esfuerzo año tras año logrando un retorno anual de 15% (razonable para mi industria) al cabo de 30 años, mi inversión tendrá un valor de:
VF = VP * (1+r) ^i
VF = 30,000 * (1+0.15) ^30
VF = 30,000 * (66,21)
VF = $ 1,986,353.16
Por supuesto que una empresa tiene muchas probabilidades de cerrar (hay mucha teoría al respecto, diciendo que 95% cierra dentro de los primeros 5 años) pero como puedo apreciar, lo que se puede lograr en términos de inversión al abrir una empresa, es realmente interesante.
Buena caza.

